The effect of particle shape on the estimation of plume height

The method of Carey and Sparks (1986) allows to estimate the height of strong plumes based on the geometry of isopleth maps. Although the method has its limitations, it is still the most used in the literature and remains important for the characterisation of eruption source parameters for eruptions that have no direct observations.

Commonly, the contouring of the lithic isopleths is preferred over the juvenile fraction because lithics are less likely to break and because the drag of smooth particles is easier to estimate. Computations behind the method of Carey and Sparks (1986) are somehow obscure and difficult to reproduce and is based on a fixed value of drag coefficient of 1.054 and the assumption of spherical particles.

The method relies on a manual plotting on downwind vs. crosswind ranges for four values of diameters/densities. For the needs of the TError package, we implemented the method of Carey and Sparks (1986) as a Matlab function in order to use it routinely and to be able to work with a continuum of particle sizes and densities (see the reference page for more details). But then, during a long flight back from Japan with my buddy Mohssen Bagheri in which the best movie Lufthansa could propose was the biopic on Jimi Hendrix (sacrilege!), we started wondering how much would the shape parameter of the particle influence the estimate of the plume height.

Method

Ok, remember that the two assumptions of the model of Carey and Sparks we would like to test are:

1. The use of spherical particles
2. The use of a fixed drag coefficient of 1.054 (note that even our method does not account for a variable drag coefficient).

Here, I won’t re-write Bagheri’s papers - which you can find at the bottom of the page - but just give an idea of the method taken.

1. For a given diameter and density, the corresponding plume height and wind speed are calculated with the method of Carey and Sparks (1986)
2. For the same diameter and density, we calculate the terminal fall velocity for a range of elongation and a flatness values as described in Bagheri and Bonadonna (2016). Note that the elongation is the ration between the intermediate and the longest axes (I/L) whereas the flatness is the ratio between the shortest and the intermediate axes (S/I) (Bagheri et al., 2015).
3. Equation 3 of Carey and Sparks is inverted to convert this terminal fall velocity to an equivalent diameter.
4. This equivalent diameter is in turn used to calculate the plume height and the wind speed through the method of Carey and Sparks (1986).

Voilà!

Results

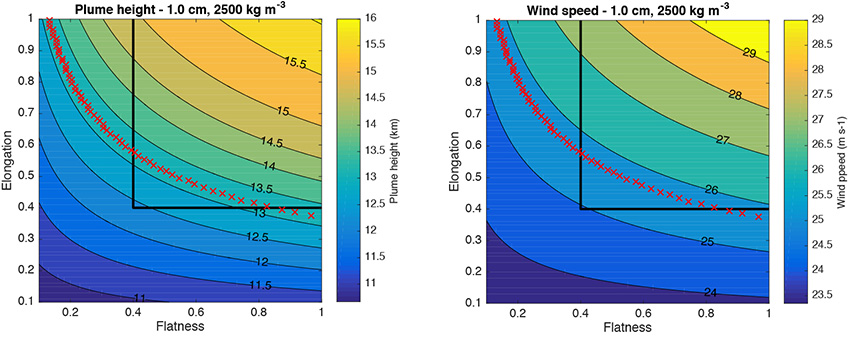
This process is implemented in a Matlab function named CareySparks86. Figure 1 shows the output of the process for elongation and flatness values ranging from 0.1 to 1.0. The square box shows the range of shapes typically relevant for volcanic lapilli (Bagheri et al., 2015) and the red curve shows a fixed value of drag coefficient of 1.054.

Recommendations

The plume height is a critical source parameter, and although recent method help estimating it more precisely when observed, older deposit still strongly depends on the method of Carey and Sparks (1986) and the characterisation of the maximum clasts. The work of Mohssen Bagheri really reduces the uncertainty on the estimation of the drag coefficient and here are the recommendations that come out of his papers for estimating an equivalent diameter:

1. For a given clast, look for the projection with the maximum area.
2. The largest axis from this projection defines L and the smallest axis defines I. Note that they do not need to be perpendicular.
3. Look for the projection with the smallest area. The smallest axis on this projection defines S.
4. Use the geometric mean of L, I and S as your equivalent diameter.

Further reading

1. Bagheri GH, Bonadonna C, Manzella I, Vonlanthen P (2015) On the characterization of size and shape of irregular particles. Powder Technol 270:141–153.
2. Bagheri G, Bonadonna C (2016) On the drag of freely falling non-spherical particles. Powder Technol 301:526–544. doi: https://doi.org/10.1016/j.powtec.2016.06.015
3. Biass S, Bagheri G, Aeberhard W, Bonadonna C (2014) TError: towards a better quantification of the uncertainty propagated during the characterization of tephra deposits. Stat Volcanol 1:1–27.
4. Carey S, Sparks R (1986) Quantitative models of the fallout and dispersal of tephra from volcanic eruption columns. Bull Volcanol 48:109–125.